コンピューターゲームで、敵がまるで人間のように賢く、絶妙な一手を選んでくる…。そんな経験はありませんか? 「どうやってコンピューターは最適な手を見つけているんだろう?」 その疑問を解き明かす鍵の一つが、今回ご紹介するMiniMax(ミニマックス)法です。
この記事を読めば、
- ゲームAIが「考える」基本的な仕組みがわかる!
- MiniMax法がAIの歴史の中でなぜ重要なのか理解できる!
- 簡単なゲームなら、自分でAIのロジックを考えられるようになるかも?
- G検定対策にも役立つ、AIの基礎知識が身につく!
AIの世界への第一歩として、そしてゲームをもっと深く楽しむために、MiniMax法の面白い世界を一緒に探検しましょう!
MiniMax法ってなに? どんなゲームで使われるの?
MiniMax法とは、簡単に言うと「最悪の事態を想定して、その中で最もマシな手を選ぶ」という考え方に基づいたアルゴリズム(計算の手順)です。特に、将棋やチェス、リバーシ、そして三目並べ(〇×ゲーム)のようなゲームで力を発揮します。
これらのゲームには共通点があります。それは「二人零和有限確定完全情報ゲーム」と呼ばれる種類のゲームであることです。ちょっと難しい言葉が出てきましたが、分解してみると簡単です。
- 二人: プレイヤーが二人(自分と相手)。
- 零和(ゼロサム): どちらかが勝てば、どちらかが負ける。引き分けはあるけど、二人の得点を合計すると常にゼロ(±0)になるような関係。(例:チェスで自分が+1点なら相手は-1点)
- 有限: ゲームが必ず終わる。(無限に続くことはない)
- 確定: サイコロのような偶然の要素がない。
- 完全情報: 相手の手札が見えない、といった隠された情報がない。盤面の状態など、全ての情報が両プレイヤーに公開されている。
MiniMax法は、このような「運要素がなく、相手の状況が全て見えている、勝敗がはっきりつく二人対戦ゲーム」で、「相手が自分にとって一番嫌な手を選んでくるだろう」と予測し、「それでも自分にとって一番損が少ない(あるいは得が大きい)手はどれか?」を見つけ出す戦略なのです。
AIの黎明期を支えた!MiniMax法の歴史
MiniMax法は、実はAI(人工知能)の研究が始まったばかりの1950年代~60年代、いわゆる「第1次AIブーム」で非常に重要な役割を果たしました。当時の研究者たちは、「人間のように考える機械」を作ることを目指し、特にチェスなどのゲームで人間と対戦できるプログラムの開発に力を入れていました。
MiniMax法は、この「ゲームをプレイするAI」の思考プロセスを初めてアルゴリズムとして形にした画期的な方法の一つでした。コンピューターが論理的に先を読み、戦略的に手を選ぶための基礎を築いたのです。G検定でも、このAIの歴史におけるMiniMax法の重要性はよく問われるポイントです。
どうやって先を読む? MiniMax法の仕組み
では、MiniMax法は具体的にどのように「先読み」をしているのでしょうか? その秘密は「ゲーム木」と「評価関数」にあります。
1. ゲームの未来を枝分かれで表現!「ゲーム木」
ゲームは、一手打つごとに状況が変わります。現在の局面から考えられる自分の手、それに対する相手の手、さらにその次の自分の手…と、可能性を枝分かれさせていくと、まるで木のような構造が見えてきます。これをゲーム木と呼びます。
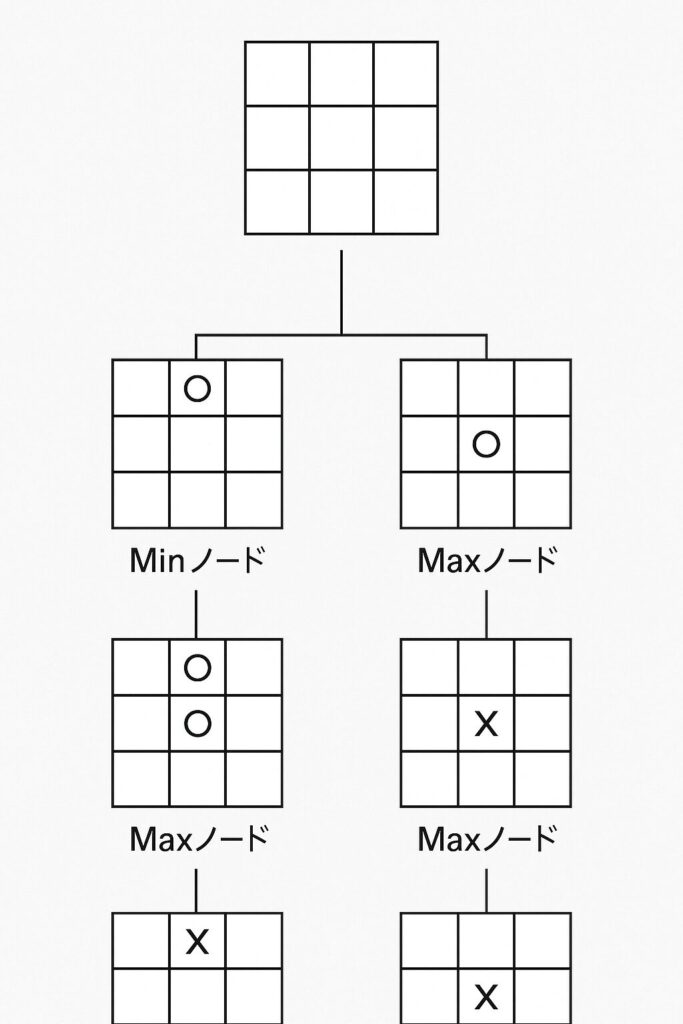
(ここに、三目並べの簡単な局面から2手先くらいまでを展開したゲーム木の図を挿入するイメージです。各ノード(局面)には簡単な盤面図を付け、自分の手番(Maxノード)と相手の手番(Minノード)が交互に現れることを示します。)
- 根 (Root): 現在の局面
- 枝 (Branch): 指し手(選択肢)
- ノード (Node): 指し手によって変化した局面
- 葉 (Leaf): ゲームの終端(勝ち、負け、引き分けが決まった局面)や、探索を打ち切る深さの局面
MiniMax法は、このゲーム木をたどって未来の局面を予測します。
2. 局面の良し悪しを点数化!「評価関数」
ゲームの途中で、どちらが有利か判断する必要がありますよね? そこで登場するのが評価関数です。これは、特定の局面を見て「この状況は自分にとってどれくらい有利(または不利)か」を点数で評価する関数です。
この点数の付け方はゲームによって様々です。
- 三目並べ: 自分の勝ちなら+1点、相手の勝ちなら-1点、引き分けなら0点、のようにシンプルに勝敗で点数化できます。
- チェス: 駒の種類ごとの価値(クイーンは9点、ポーンは1点など)の合計、盤面の支配度、キングの安全性などを組み合わせて点数化します。
- 将棋: 駒の損得だけでなく、持ち駒の種類や価値、玉の囲いの固さ、相手の玉への迫り具合なども考慮します。
- リバーシ: 単純な石の数だけでなく、隅を取れているか、辺を確保できているか、相手が打てる場所を制限できているか、などが評価のポイントになります。

もしあなたがオリジナルの〇×ゲームAIを作るとしたら、どんな評価関数を考えますか? 勝敗だけでなく、例えば「リーチ(あと一手で揃う状態)」にも点数をつけたりすると、より強いAIになるかもしれませんね!
3. 最善手を選ぶ! Min と Max の考え方
ゲーム木と評価関数を使って、いよいよMiniMax法の核心部分です。
- 自分の手番 (Maxノード): 自分の目的は、評価値を最大 (Max) にすることです。ゲーム木で次に進める複数の選択肢(子ノード)の中から、評価値が最も高くなる手を選びます。
- 相手の手番 (Minノード): 相手は自分にとって最悪の手、つまり評価値を最小 (Min) にしてくる、と仮定します。ゲーム木で次に進める複数の選択肢の中から、評価値が最も低くなる手を相手が選ぶと考えます。
MiniMax法は、ゲーム木の末端(葉)から根に向かって、このMaxとMinの考え方を交互に適用しながら評価値を計算していきます。
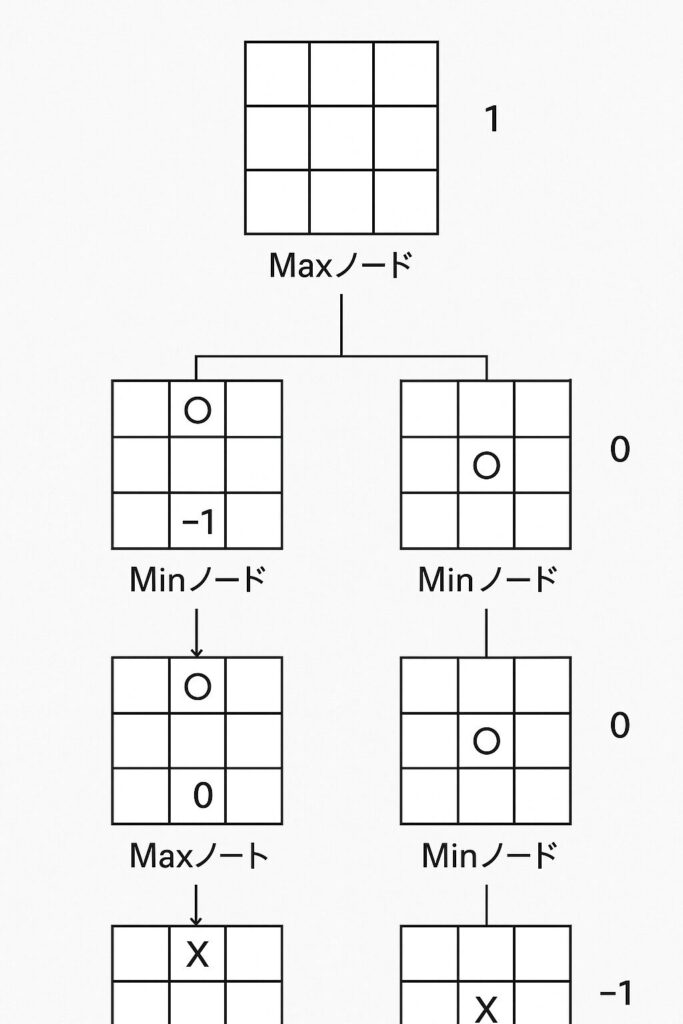

ここに、先ほどの三目並べのゲーム木に評価値を書き込み、末端ノードの評価値(+1, -1, 0)から、Minノード、Maxノードのルールに従って親ノードへと評価値が伝播していく様子を矢印などで示す図を挿入するイメージです。Maxノードでは子の最大値を、Minノードでは子の最小値を選んでいることを明確にします。
このプロセスを経て、現在の局面(根ノード)から伸びる最初の手のうち、最終的に最も高い評価値につながるものが、MiniMax法によって選ばれる「最善手」となります。
MiniMax法を動かしてみよう(擬似コード)
少し専門的になりますが、MiniMax法の動きをプログラムの形で見てみましょう。これは擬似コードと呼ばれる、プログラムの動きを簡略化した表現です。
// position: 現在の局面
// depth: あと何手先まで読むか(探索の深さ)
function Minimax(position, depth):
// 探索の深さに達したか、ゲームが終了したら、評価関数で局面を評価して返す
if depth == 0 or is_game_over(position):
return evaluate(position)
// 自分の手番 (Max) の場合
if is_my_turn(position):
max_eval = -無限大 // とりあえず最小値を入れておく
// 次の可能な手をすべて試す
for each move in possible_moves(position):
next_position = make_move(position, move)
eval = Minimax(next_position, depth - 1) // 再帰的に呼び出す
max_eval = max(max_eval, eval) // より良い手が見つかれば更新
return max_eval
// 相手の手番 (Min) の場合
else:
min_eval = +無限大 // とりあえず最大値を入れておく
// 次の可能な手をすべて試す
for each move in possible_moves(position):
next_position = make_move(position, move)
eval = Minimax(next_position, depth - 1) // 再帰的に呼び出す
min_eval = min(min_eval, eval) // より悪い手が見つかれば更新
return min_evalこのコードは、Minimax関数が自分自身を呼び出す「再帰」という仕組みを使って、ゲーム木を深く探索していく様子を表しています。自分の手番なら最大値(max)を、相手の手番なら最小値(min)を選んで、評価値を返していますね。
MiniMax法の弱点:膨大な計算量
MiniMax法は理論的には最適ですが、大きな弱点があります。それは、計算量が非常に多くなることです。
ゲームが進むにつれて、ゲーム木の枝分かれは爆発的に増えていきます。例えば、将棋では1つの局面から考えられる手は平均80通りほどあり、数手先を読むだけでも天文学的な数の局面を評価しなければならなくなります。全ての可能性を調べ上げるのは、どんなに速いコンピューターでも現実的ではありません。
そのため、実際のゲームAIでは、読む手の深さ(depth)を制限して、計算時間を現実的な範囲に収めるのが一般的です。
計算を速く! αβ(アルファベータ)法による効率化
MiniMax法の計算量問題を改善するために考え出されたのが、αβ(アルファベータ)法です。これは、MiniMax法と同じ結果を得ながら、明らかに無駄な探索を省略(枝刈り)することで、計算時間を大幅に短縮するテクニックです。
αβ法の核心は、「この手を評価しても、どうせ最終的な結果には影響しないな」と判断できる枝(局面の連なり)を見つけ出し、その先の探索をバッサリ切り捨てる点にあります。
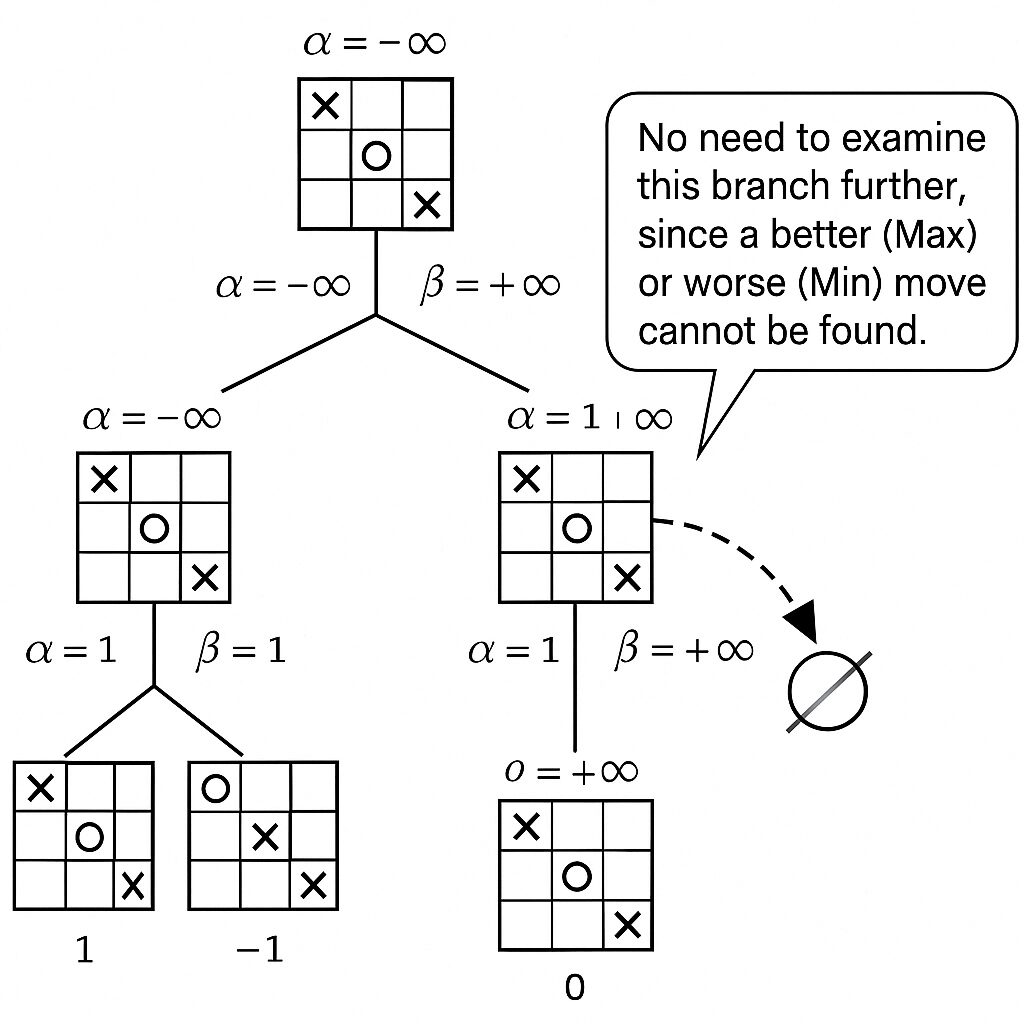

αβ法を使うことで、MiniMax法単体よりもはるかに深くゲーム木を探索できるようになり、より強いAIを作ることが可能になります。
さらに先へ:必勝読みと完全読み
リバーシのように、勝敗だけでなく石差が重要なゲームもあります。このような場合、単に勝ち負けだけを読む「必勝読み」と、最終的な点差(石差)まで正確に読み切る「完全読み」という考え方があります。完全読みはさらに計算量が膨大になりますが、実現できれば完璧なプレイが可能になります。
MiniMax法の現代における意義と発展
MiniMax法は古いアルゴリズムですが、その考え方は現代のAI技術にも脈々と受け継がれています。
- 強化学習との関連: AIが試行錯誤しながら最適な行動を学習する「強化学習」の中でも、将来の報酬を最大化するための探索戦略の基礎として、MiniMax法の考え方が応用されています。
- ゲームAIの進化: チェスで世界チャンピオンを破ったDeep Blueや、囲碁でトップ棋士を破ったAlphaGoなどの強力なゲームAIも、MiniMax法のような探索アルゴリズムを基礎としつつ、機械学習などのより高度な技術を組み合わせて実現されています。
MiniMax法を理解することは、これらの現代AI技術への扉を開く第一歩と言えるでしょう。
次のステップへ:さらにAIの世界を探求しよう
MiniMax法やαβ法を知ると、さらに高度な探索アルゴリズムにも興味が湧いてくるかもしれません。
- モンテカルロ木探索: 近年の囲碁AIなどで大きな成果を上げたアルゴリズム。ランダムなシミュレーションを多数行うことで有望な手を見つけ出す手法です。
- 強化学習: AI自身がプレイ経験を通じて学習し、戦略を獲得していく手法。ゲームAIだけでなく、ロボット制御など幅広い分野で活用されています。
これらを学ぶことで、AIがどのように「賢さ」を獲得していくのか、さらに深く理解できるはずです。
まとめ:MiniMax法から広がるAIの世界
今回は、ゲームAIの基本的な思考アルゴリズムであるMiniMax法について、その仕組みから歴史、応用、そして限界と発展までを解説しました。
- MiniMax法は「最悪を想定し最善を選ぶ」戦略。
- 「二人零和有限確定完全情報ゲーム」で特に有効。
- AI黎明期を支えた重要なアルゴリズム。
- 「ゲーム木」と「評価関数」を使って先を読む。
- 計算量問題を解決するために「αβ法」がある。
- 現代のAI技術にもその考え方は生きている。
MiniMax法はシンプルながらも奥深く、AIの探索と推論の基本を学ぶ上で非常に重要です。この記事が、あなたのAIへの興味関心をさらに深めるきっかけとなれば幸いです。
あなたが好きなゲームで、MiniMax法やその考え方がどのように使えそうか、あるいはどんな評価関数が良いか、ぜひコメントでアイデアを教えてください!

コメント